Lamb(兰姆)波是二维波,与三维体波相比具有衰减速度慢,传播距离远的特点,因此常被用于大型板材的长距离及快速无损检测中.板材中兰姆波与管中、变截面波导介质中的导波一样,具有频散性与多模态性.加上环境噪声等多方面因素的影响,导波检测时传感器接收到的Lamb波信号非常复杂,属于非平稳随机信号,需要利用有效的信号处理技术提取有用的信息成分才能确定合适的激励方式,获得更好的检测成像效果.传统的处理Lamb波信号的方法包括反射系数法、傅里叶变换法、小波变换法、动态光弹法等,但是这些方法都有各自的不足.反射系数法是通过测量漏兰姆波的频散曲线来确定材料的性质,但测量难度较大.傅里叶变换只能处理线性非平稳的信号.小波变换法虽然在理论上能处理非线性非平稳信号,但是同傅里叶变换、短时傅里叶变换法一样,都受Heisenberg测不准原理制约,即时间窗口与频率窗口的乘积为一个常数,这就意味着如果要提高时间精度就得牺牲频率精度,反之亦然.当兰姆波中不同模态的频率比较接近时,不适用小波变换处理信号.动态光弹法能从Lamb波的应力分布观察到传播和频散,但是在实际检测中对硬件要求较高.

 

　　HilbertＧHuang变换(HHT)是一种近几年发展起来的一种自适应信号处理方法,不受Heisenberg测不准原理制约,可以在时间和频率上同时达到很高的精度,非常适用于分析突变信号.笔者以薄壁铝板为研究对象,利用双重时间尺度的方法,即采用二维傅里叶变换法整体传播时间尺度,HilbertＧHuang变换从单一信号时间尺度,将二者相结合对在铝板中不同位置采集到的Lamb波信号作数据处理与分析,与半解析有限元法得到兰姆波的频散曲线相对照,进而识别与分析铝板中兰姆波模态,获得较高的时间分辨率.

　　１薄板中超声导波分离模态信号分析方法

　　１．１传播特性的半解析有限元分析

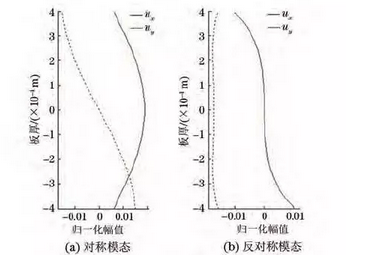
　　在边界自由的固体板中,板材厚度与激励声波波长数量级相当时,在板中产生的应力波就是Lamb波.根据薄板两表面质点振动相位关系,Lamb波分为对称型Lamb波和反对称型Lamb波,分别用Sn、An表示,n为模态的阶次(n＝０,１,２,３